Total Knee Arthroplasty Optimization
View on GitHub 
Total Knee Arthroplasty (TKA) is a complete replacement of the knee joint using a prosthesis. TKA is a very common operation with high success rates, but careful consideration must be given to the materials and design of the prosthesis to ensure it can withstand intense biomechanical stresses for several years.
A polyethylene layer as the articulating surface is the gold standard since it allows the femoral and tibial components to function smoothly, but polyethylene wear is the most common cause for TKA failure. Reducing stresses on this layer is important for improving longevity, which is why all geometric variables must be considered in the design. In this project the stresses and strains induced by different polyehthylene thicknesses and different loading cases are analyzed. The geometric design of the prosthesis can be optimized using MATLAB’s Optimization Toolbox, inputting 6 variables of tibial tray material thicknesses and sagittal and frontal radii of the femoral and tibial components and outputting the values which minimize the stresses.
Cases
Analysis is first performed on the bending stresses and the strains from different material thicknesses and loading cases.
The loading cases are represented as two forces, centered at points 1/4 and 3/4 along the width of the prosthesis:
- Habitual
- 1500N at each point
- Extreme
- 2500N at one point, 500N at one point
The material thicknesses analyzed, using ultra-high-molecular-weight polyethylene (UHMWPE) and a cobalt-chromium alloy (Co-Cr) are:
- UHMWPE - 11mm, CoCr - 1mm
- UHMWPE - 8mm, CoCr - 4mm
- UHMWPE - 5mm, CoCr - 7mm
Results
The bending stress, seen from a frontal view with habitual loading, and UHMWPE thicknesses of 5mm and 11mm:
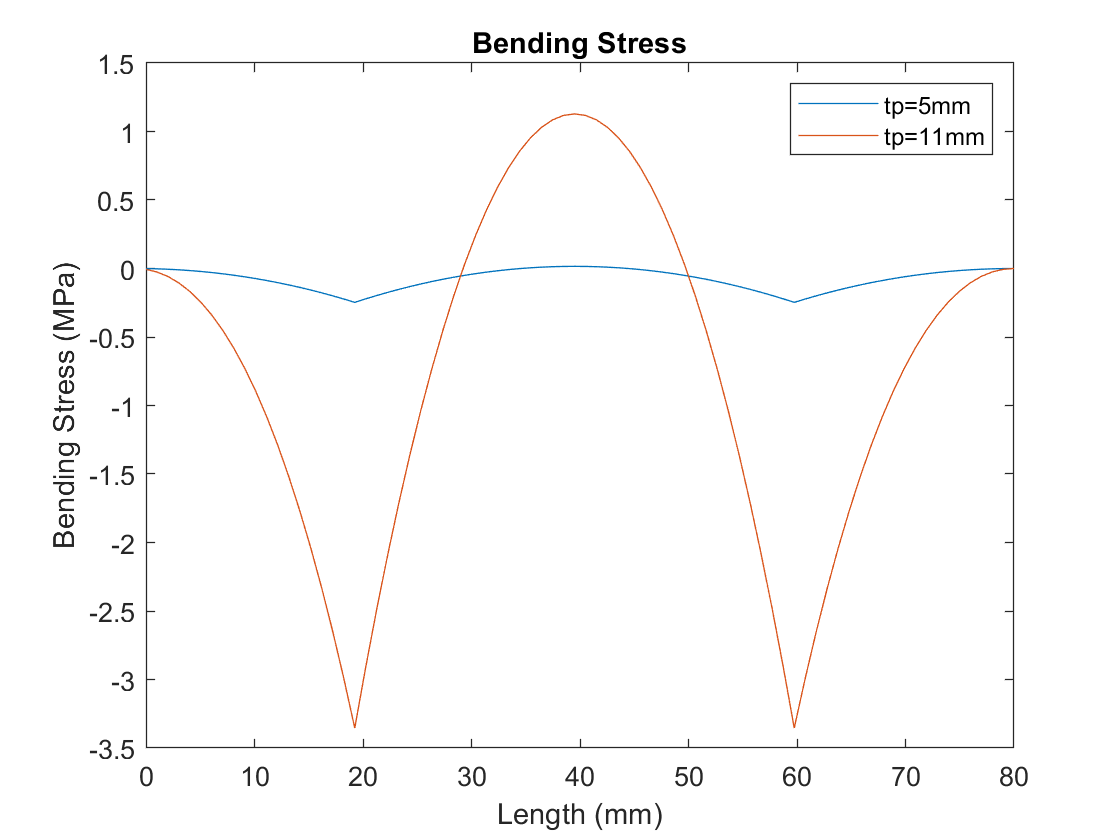
The UHMWPE component displays rigid and flexible beam behavior when the corresponding Co-Cr thickness is greater and lesser, respectively. Bending stresses are seen to be lesser with a lesser UHMWPE thickness.
Strains on the trabecular bone for the different thicknesses, and for each loading case, can be plotted:
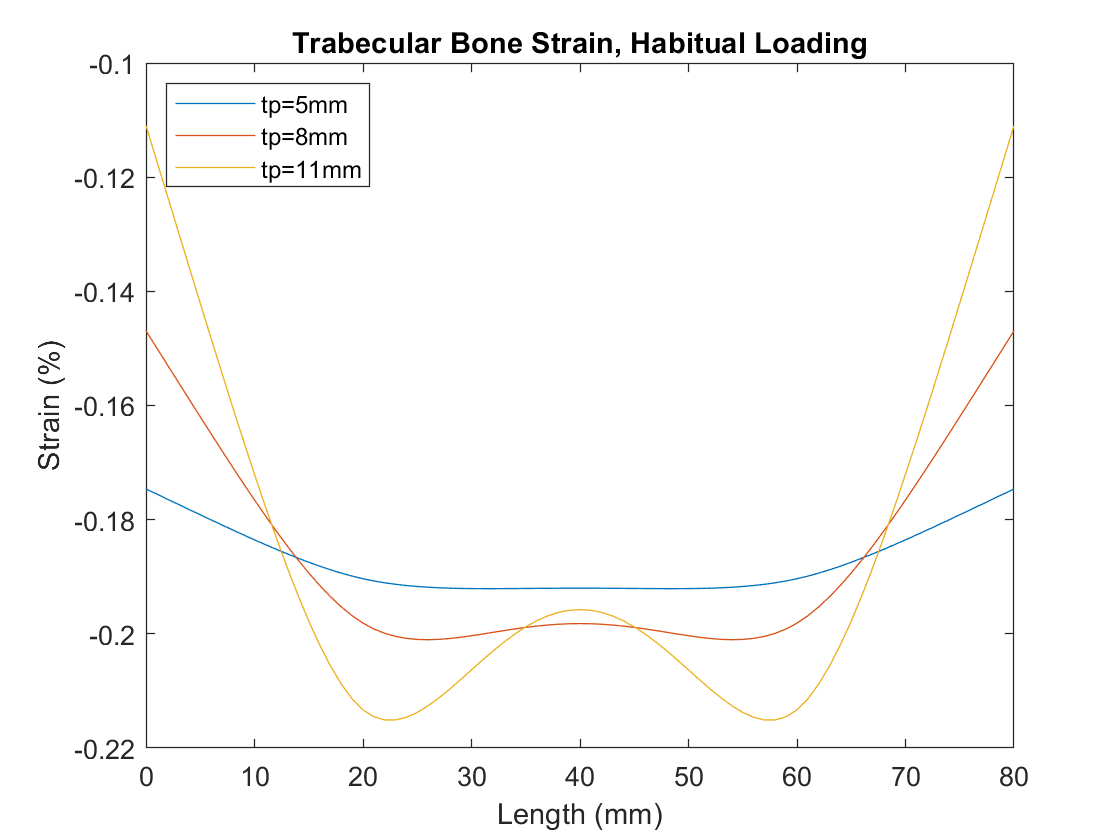
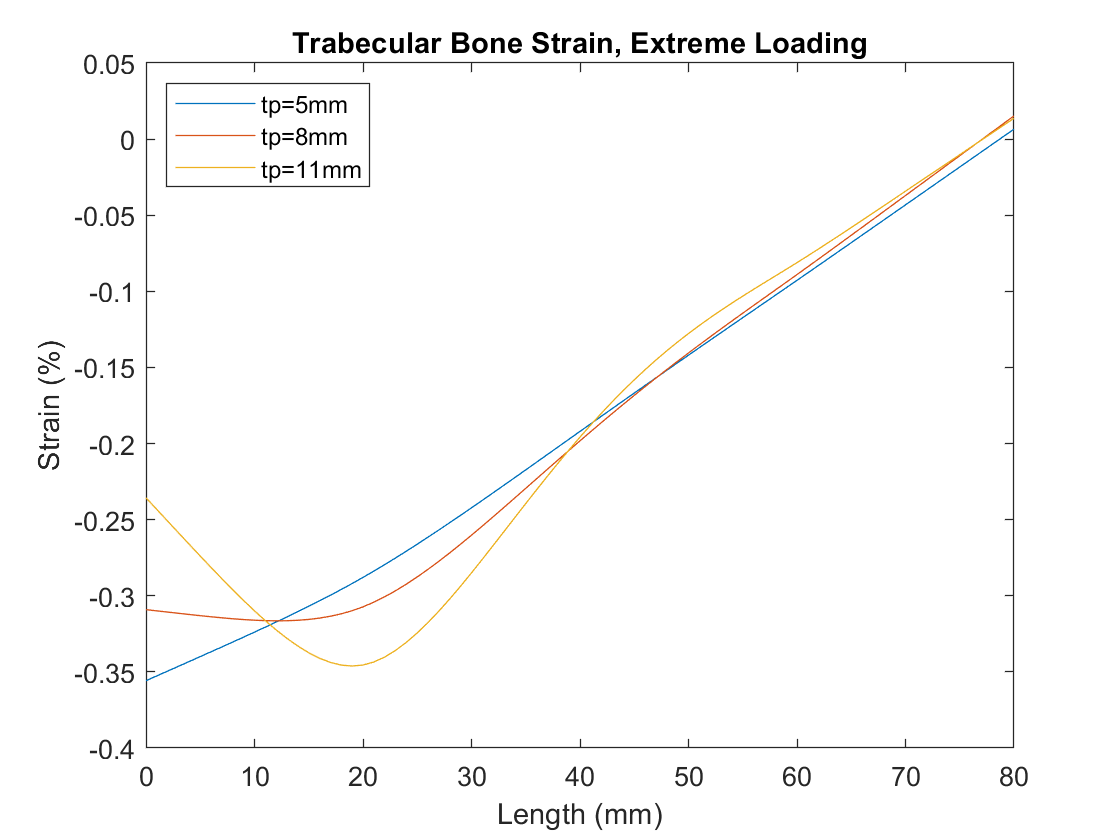
Von Mises stresses for the cases can also be calculated:
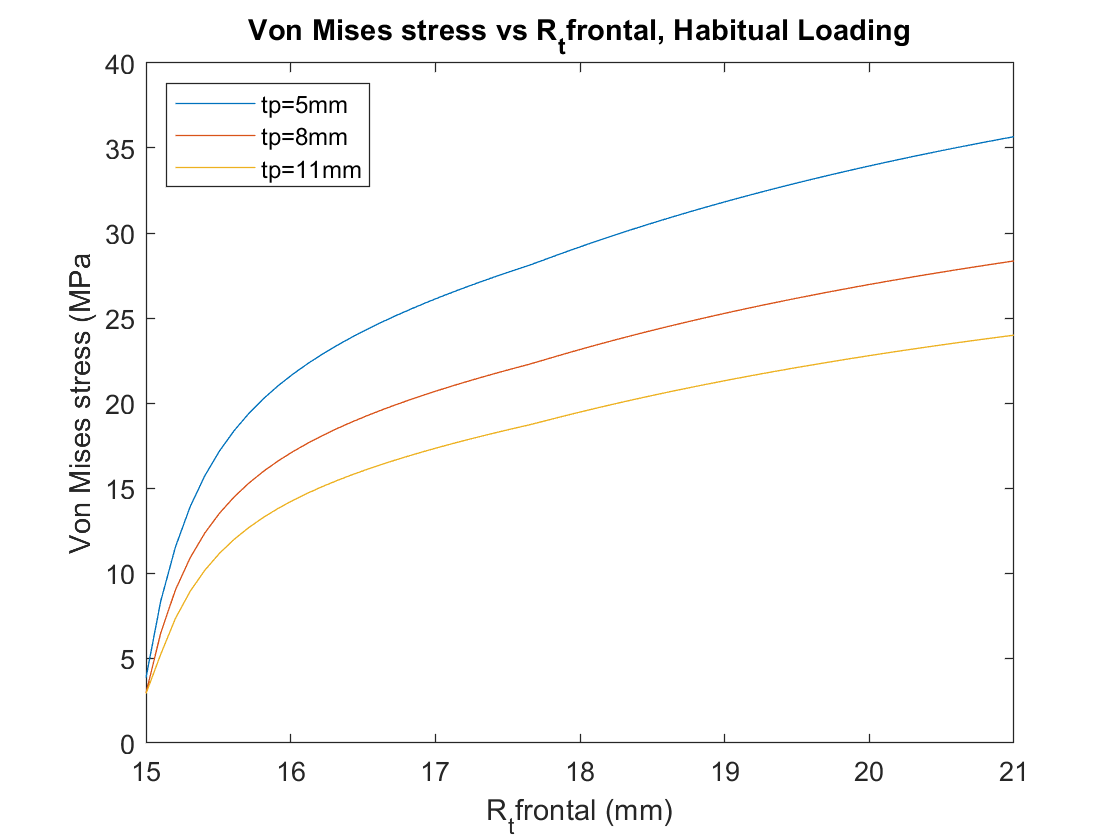
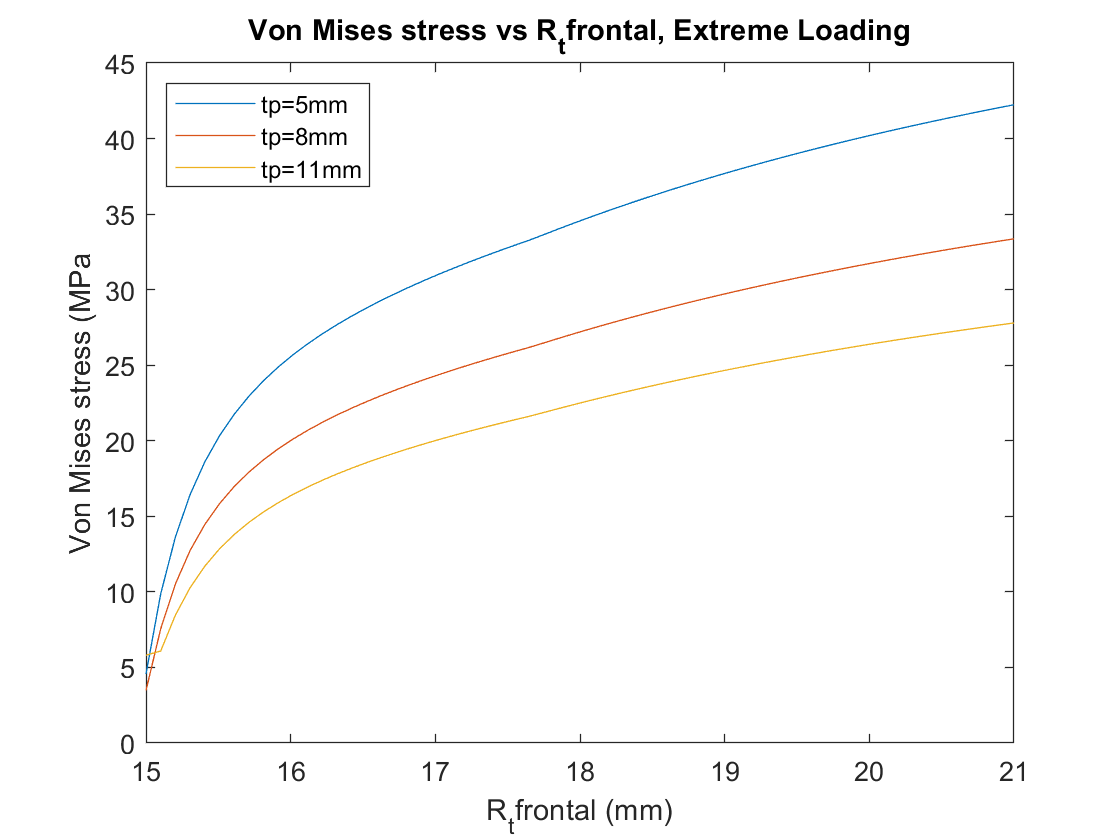
Insight from these analyses can be used to pick a lesser UHMWPE thickness, and optimize the remaining geometric variables to minimize stresses caused by both of these loading cases to ensure the design can withstand both habitual and extreme loading.
